Introduction
In this project, I explored the concepts of "morphing" faces into other faces and figuring out the "average" face of populations. I used an image of myself and morphed it into different images of other people and into the average face shape of a population.
Part 1: Defining Correspondences
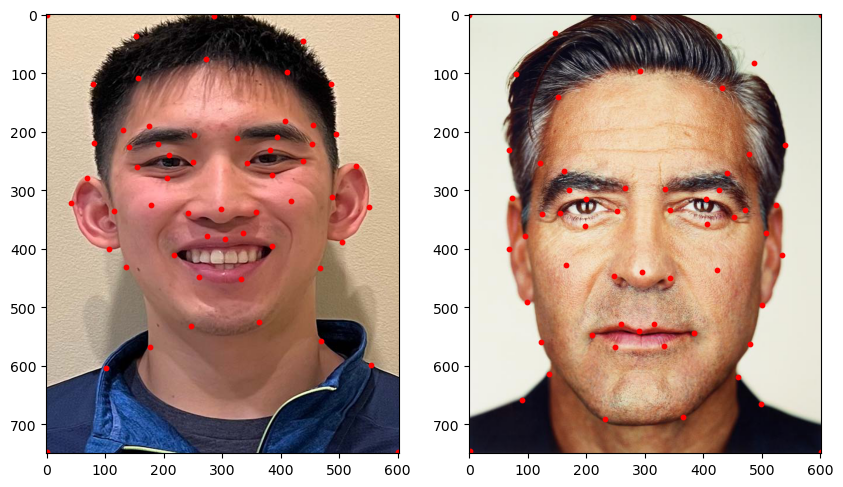
To begin to morph my face into another person's face, we first must ensure the images line up with each other. This is done by defining corresponding points on both images and then proceeding to warp our images into the same "shape." We do this by manually choosing points corresponding to relevant features of our portrait, and then using these points to define a triangulation. We can then determine a transformation matrix to warp our triangles to our desired geometry.
I implemented this using ginput from the matplotlib library to allow me to click on points on the image. I then used a Delaunay Triangulation to define triangles since this will not produce overly skinny triangles.
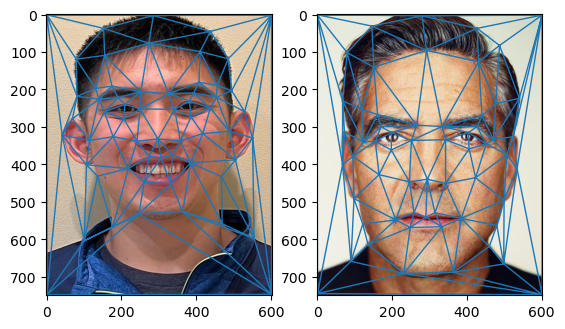
I did this on the average of the landmark points between the images I wanted to morph so that it would be the same triangulation for both images. Here are my points I plotted and the resulting triangulation:
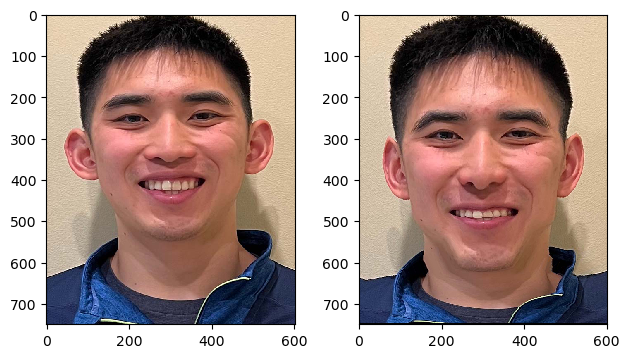
Part 2: Computing the "Mid-Way Face"
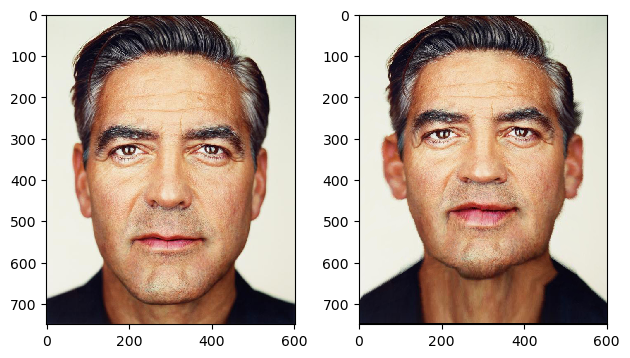

Part 3: The Morph Sequence
We can now produce a smooth warp between our two images using a very similar process as we did for creating the "mid-way" face. Producing a morph sequence is the same thing as producing intermediate images of the two faces morphed to each other according to some factor of how much of each we want to moprh at that point. We can use the same inverse transform function used in Part 2 with goal points being some linearly interpolated point between the two sets of keypoints. Here is the result of the morph sequence between my face and George Clooney's face:

Part 4: The "Mean Face" of a Population
We can now compute the "mean face" of a population by averaging the keypoint locations of a set of images and then morphing all the images to this mean face. This is done by averaging the keypoint locations of all the images and then morphing all the images to this mean face. We can then achieve our mean face by averaging all of these morphed images. The dataset I used for this was the FEI Face Database, and I used spatially normalized, frontal images from this dataset. In creating this mean face, I warped each face into the average shape. Here are some examples of that:


Here is the result of the "mean face" of the population:

I also played around with warping my face to match the average shape and the average shape to match my geometry:


Part 5: Caricatures
We can also extrapolate from the population averages to create caricatures. We can use the mean we calculated in the previous part to extrapolate features from myself using the formula: \[\text{extrapolated} = \text{average} + \alpha \cdot \text{img}\] Where we are performing our operations pixel by pixel and alpha is a parameter controlling how much extrapolation we perform. Here are the results of creating caricatures of myself for differing values of alpha:

Bells and Whistles: PCA Basis
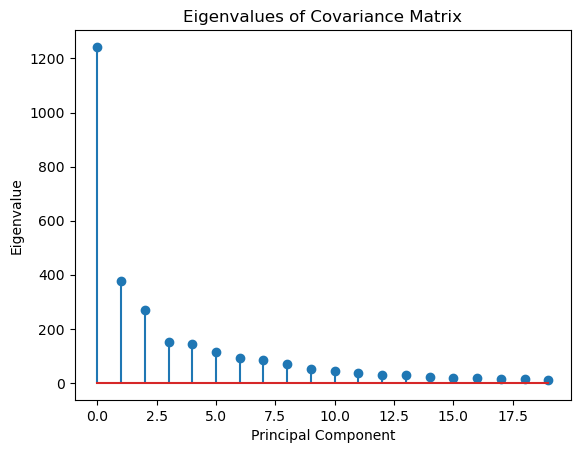
We can construct a PCA basis for the keypoints of all of the images. This is the basis that best captures the variance in the data. While we initially zero-mean our data before constructing our PCA basis, we can better visualize the basis by adding back the mean and showing the landmark points on the average face. We can see that most of these keypoints look the same, which is most likely due to the fact that all of these images in the dataset were already transformed to have features in very similar places. We can also visualize the variance captured by the PCA basis by looking at the eigenvalues associated with each PCA vector.

We can now use this PCA basis to perform transformations such as the caricatures we did in Part 5.

Comparing our original caricatures to our PCA caricatures, it seems like our PCA caricatures do not extrapolate quite as much as our original.
