Part 1: Fun with Filters
Finite Difference Operator
A common task in image processing is finding the edges in an image along both the horizontal and vertical directions. This is often done by computing the gradients of the image along the x and y directions.
This can be simply done by convolving the image with simple kernels that approximate the derivative of the image using finite differences. These kernels are simply taking the difference between two consecutive pixels in the image as an approximation of the true derivative.
$$\text{Gradient in x direction: } \matrix{D_x} = \begin{bmatrix} 1 -1 \end{bmatrix}$$
$$\text{Gradient in y direction: } \matrix{D_y} = \begin{bmatrix} 1 \\ -1 \end{bmatrix}$$

 We can also compute the magnitude of the gradient by taking the square root of the sum of the squares of the gradients in the x and y directions to visualize the edges in the image.
In order to remove some of the noise, we also can threshold the gradient magnitude to get a clearer picture of the edges in the image.
We can also compute the magnitude of the gradient by taking the square root of the sum of the squares of the gradients in the x and y directions to visualize the edges in the image.
In order to remove some of the noise, we also can threshold the gradient magnitude to get a clearer picture of the edges in the image.



Image Gradient (dx)

Image Gradient (dy)

Image Gradient Magnitude

Thresholded Image Gradient Magnitude (threshold=0.27)
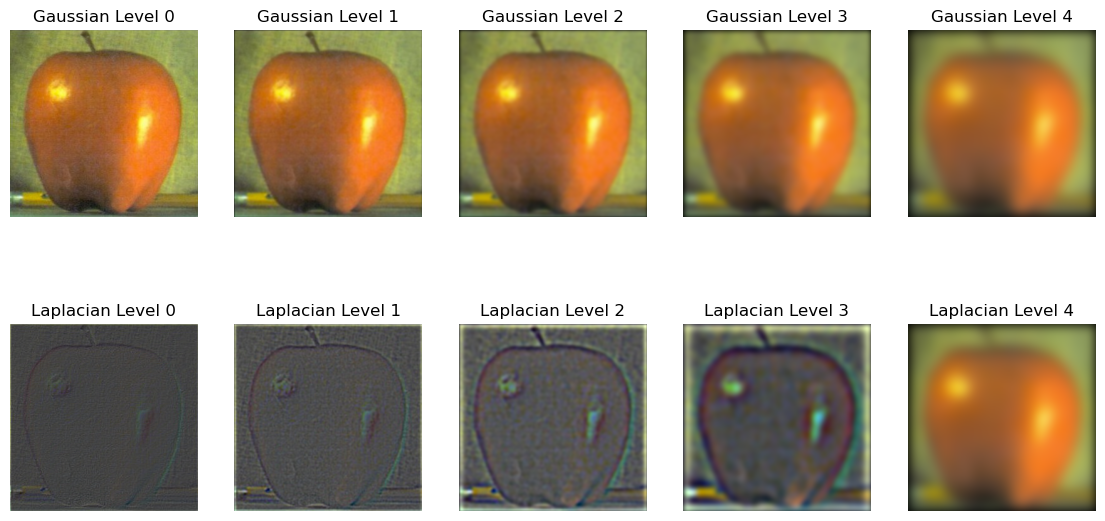
Derivative of Gaussian (DoG) Filter
We can also smooth out our gradient magnitude edges by smoothing image first using a Gaussian filter. Convolving our image with a Gaussian filter gives us a cleaner picture of the edges.
When we thresholded, we could tell we were only displaying the stronger edges and there was less noise in the image. However, there were also some gaps in the edges that we did have due to this thresholding.
We can see in the smoothed version that the edges are more continuous and there are less gaps in the edges.

 Due to the linear nature of convolutions, we can also compute this smoothed gradient magnitude using only one filter instead of two. This filter is known as the Derivative of Gaussian (DoG) filter and works by convolving the Gaussian with the finite difference operators first.
Since these are much smaller than the image, we can convolve the Gaussian with the finite difference operators first and then convolve the result with the image to get the same result in less time.
Due to the linear nature of convolutions, we can also compute this smoothed gradient magnitude using only one filter instead of two. This filter is known as the Derivative of Gaussian (DoG) filter and works by convolving the Gaussian with the finite difference operators first.
Since these are much smaller than the image, we can convolve the Gaussian with the finite difference operators first and then convolve the result with the image to get the same result in less time.



Thresholded Image Gradient Magnitude (non-smoothed)

Thresholded Image Gradient Magnitude (smoothed)

Two Convolutions

Single Convolution (DoG filter)