Neural Radiance Fields

For my final project, I choose to implement a Nerual Radiance Field (NeRF) model in order to render 3D scenes. NeRF is a method that can render novel views of a scene by learning a continuous function that maps 3D coordinates to RGB and density values. This allows for the generation of photorealistic images of 3D scenes from a small number of images. The model is trained on a dataset of images and corresponding camera poses, and can then be used to render novel views of the scene. I based a lot of this project on the original NeRF paper.

In the first part, of this project, I started by developing my understanding of Neural Fields by implementing a 2D version of the model. The goal of this part was to fit a Neural Field to 2D images where we do not need to worry about radiance. Our system simplifies down to just having to implement a filed \(F: \{u, v\} \rightarrow \{r, g, b\}\) that maps 2D pixel coordinates to RGB values. We can do this by using a Multilayer Perceptron (MLP) network with Sinusoidal Positional Encoding (PE) that takes in a two dimensional input and outputs a three dimensional value (pixel color).

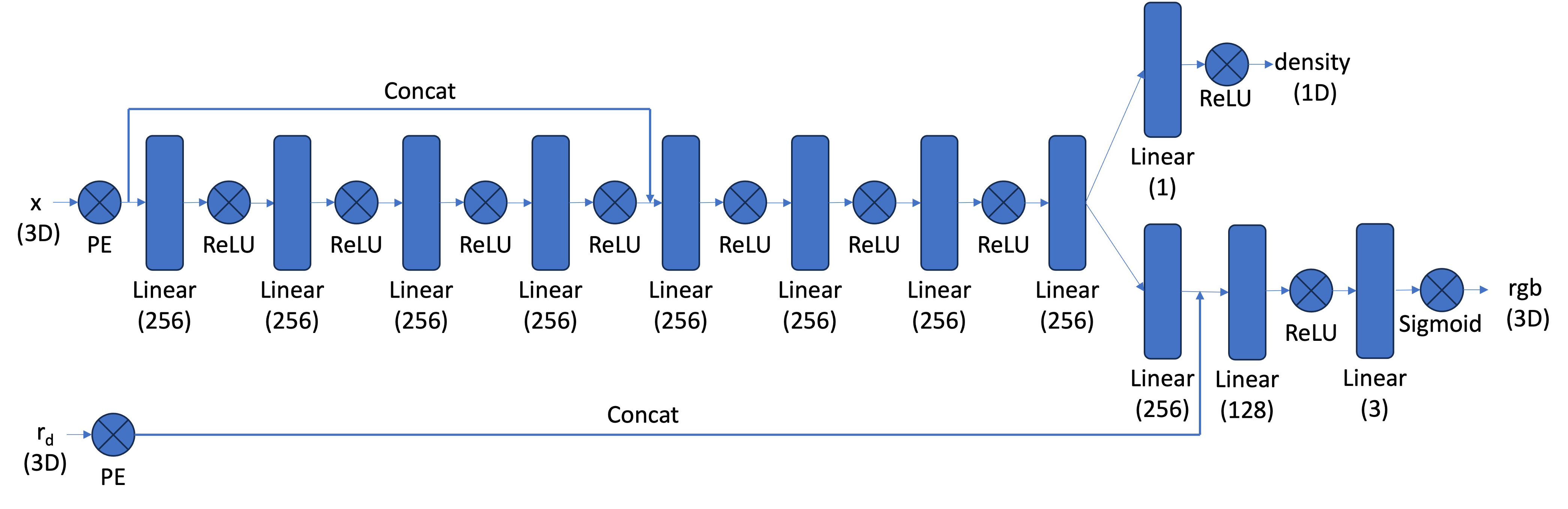
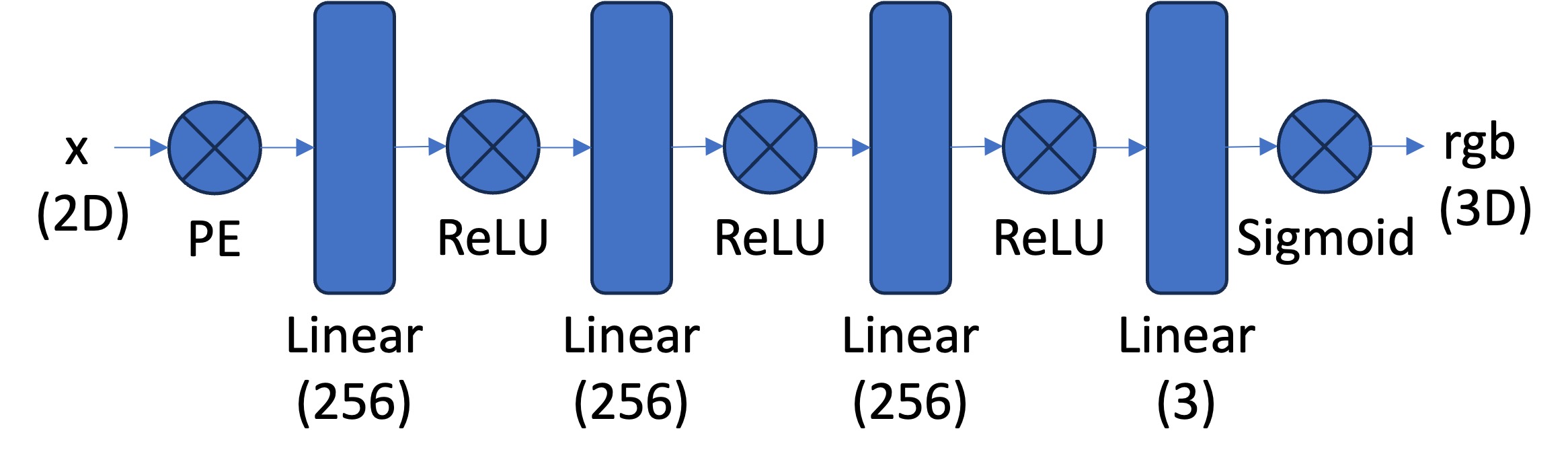
Model Architecture:

The network is composed of a couple fully connected layers followed by a ReLU activation function. One of the more interesting parts of this model architecture is the use of the Sinusoidal Positional Encoding (PE). This is an operation you apply to the input that expands the dimensionality of the input by adding sinusoidal functions of different frequencies. This allows the model to learn higher frequency patterns in the data based on the max frequency level \(l\) we choose. \[ PE(x) = \{x, \sin(2^0\pi x), \cos(2^0\pi x), \sin(2^1\pi x), \cos(2^1\pi x), \ldots, \sin(2^{L-1}\pi x), \cos(2^{L-1}\pi x)\} \]

Our overall architecture is as follows: (we use a Sigmoid activation at the function to constrain our output range to \((0, 1)\) to match valid pixel colors.)

Dataloader

The first step in our process of training our 2D Neural Field is to generate data to train on. Since the images we want to work with are a little bit too high resolution to train with all of our pixels, we randomly sample \(N\) pixels from our image during every training iteration. We can do this all within our dataloader, which will return both the \((N \times 2)\) pixel coordinates and the corresponding \((N \times 3)\) RGB values of the pixels. These will be our inputs and supervision targets to our model we will use to train. We will also normalize both of these values before inputting them into our model.

Training

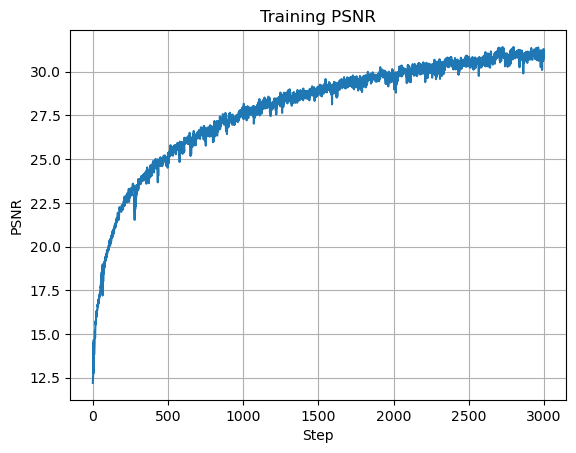
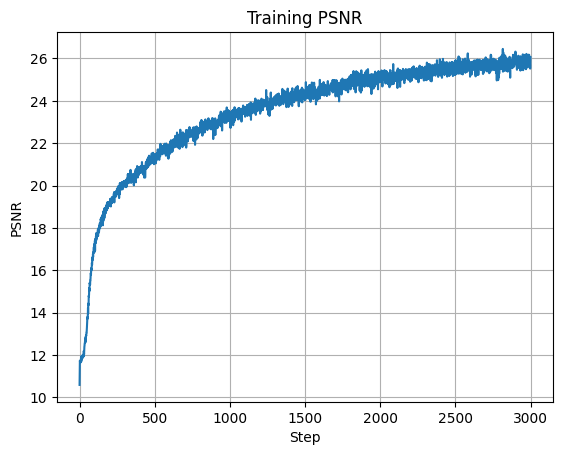
We will train our model using the mean squared error (MSE) loss function and an Adam optimizer with learning rate \(0.01\). We will run our model for \(2000\) iterations with a batch size of \(10,000\) and a max frequency level of \(L=10\). Also, instead of using the MSE as our metric, we will display the Peak Signal-to-Noise Ratio (PSNR) of our model's output compared to the ground truth image. This is the more common metric used for measuring reconstruction quality of an image, and easy to calculate from the MSE. If an image is normalized to \([0, 1]\), then the PSNR is simply: \[ PSNR = 10 \cdot \log_{10}\left(\frac{1}{\text{MSE}}\right) \] Here are the results of our initial training, with visualizations of the model's output during different stages of training.

As we can see, our model is able to learn the underlying structure of the image and produce a reasonable reconstruction of the image. The PSNR of our final output is \(26.325\), which is a decent reconstruction of the image.

Hyperparameter Tuning

We can better understand how our model works by adjusting the hyperparameters of our model. We can try to see how the model performs with different max frequency levels, different numbers of layers, and different numbers of neurons in each layer. While our image reconstruction was quite good, we can also use hyperparameter tuning to attempt to get a better image reconstruction.

Max Frequency Level:

The max frequency level in our model corresponds to the dimensionality of our positional encoding. I tested decreasing the max frequency levels to see the effects of adjusting the dimensionality of our input. As seen in the following images, the model is able to learn the underlying structure of the image with lower frequency levels, but the details are clearly left out of the image without a high enough max frequency level.

Number of Hidden Layers

In a Multilayer Perceptron model, we have a bunch of fully connected layers that are connected to each other through activation functions. The first fully connected layer is the inpuit layer, the last is the output layer, and all of the others in between are known as hidden layers. Our initial architecture had \(2\) hidden layers, but we can try to adjust the number of layers to determine how that affects our model's performance.

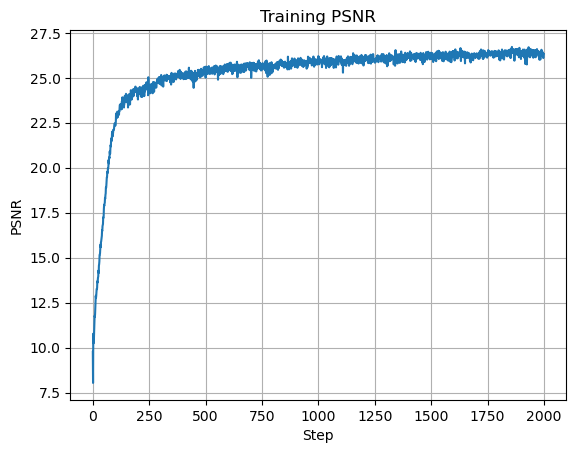
We can see that with more hidden layers, our model becomes more complex and is better able to learn our input image. However, one thing to note is that with more hidden layers, there is more to learn, and I had to increase the number of iterations and decrease the learning rate to get the model to begin to converge. Here is our best model with \(10\) hidden layers, a learning rate of \(0.001\), and \(3000\) iterations which achieved a PSNR of \(28.189\):

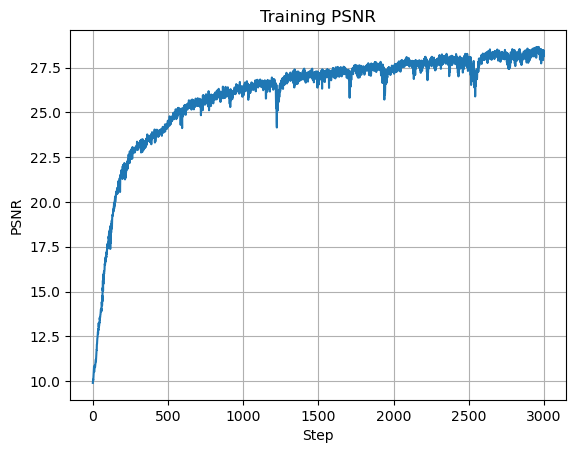
Number of Hidden Units

The number of hidden units in a layer is the number of neurons in that layer, or the number of parameters that the model can learn. We can adjust the number of hidden units to see how that affects our model's performance. In our original model, we used \(256\) hidden units in each layer, but we can try to adjust this number to see how it affects our model's performance.

Similarly to the number of hidden layers, I also had to decrease the laerning rate and increase the number of iterations in order to get the model loss to converge (I used a learning rate of \(0.001\) and \(3000\) iterations to train all of these models). This is once again because increasing the number of hidden units increases the complexity of our model, and thus requires more iterations to learn the underlying structure of the image. We can see that increasing the number of hidden units allows the model to perform better. Here is my best model which used \(512\) hidden units and achieved a PSNR of \(27.696\):

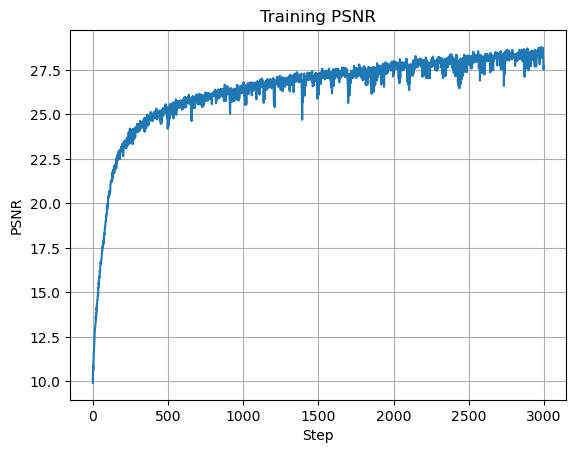
Conclusion

From this hyperparameter testing, we can see that increasing the max frequency level, the number of hidden layers, and number of hidden units all help to improve the model's ability to reconstruct the image. However, these all come with tradeoffs, as epecially for the latter two, increasing the model complexity increases the training time. Taking this into account, I decided on the configuration of a max frequency level of \(10\), \(7\) hidden layers, and \(512\) hidden units with a learning rate of \(0.001\) and \(3000\) iterations to try our model on another image:

In the second part of this project, I implemented a 3D version of the Neural Radiance Field model. The goal of this part was to fit a Neural Radiance Field to a 3D scene from multiple images and camera poses to allow me to generate novel views of the scene. I used the same dataset from the original NeRF paper, except with slightly lower resolution images due to the computational resources available to me.

2.1: Creating Rays from Cameras

Camera to World Coordinate Conversion

The first step in implementing the 3D version of our Neural Radiance Field was to create helper functions for allowing us to define the rays that we will use to sample our scene. The first function we need is one that will help us convert between the camera frame \(\mathbf{X}_c = (x_c, y_c, z_c)\) and the world frame \(\mathbf{X}_w = (x_w, y_w, z_w)\). We can do this using a rotation matrix and translation vector: \[ \begin{bmatrix} x_c \\ y_c \\ z_c \end{bmatrix} = \begin{bmatrix} \mathbf{R}_{3\times3} & \mathbf{t} \\ \mathbf{0}_{1\times3} & 1\end{bmatrix} \begin{bmatrix} x_w \\ y_w \\ z_w \\ 1 \end{bmatrix} \] The conversion matrix \(\begin{bmatrix} \mathbf{R}_{3\times3} & \mathbf{t} \\ \mathbf{0}_{1\times3} & 1\end{bmatrix}\) is called the world-to-camera (w2c) transformation matrix, or extrinsic matrix. The inverse is called the camera-to-world (c2w) transformation matrix, and as their names suggest, they are used to convert coordinates between the two different frames. I implemented this function transform(c2w, x_c) to convert from camera to world coordinates. I also made sure to implement this function using numpy and the np.einsum function to allow for batched dimensions.

Pixel to Camera Coordinate Conversion

We also need one more coordinate transformation between the 2d pixel coordinates into the camera coordinates. In order to determine this, we consider a pinhole camera model with focal length \(f_x, f_y\) and camera center \((o_x = \frac{\text{image_width}}{2}, o_y = \frac{\text{image_height}}{2})\). Given this info about the camera, we can construct the camera intrinsic matrix \(\mathbf{K}\): \[ \mathbf{K} = \begin{bmatrix} f_x & 0 & o_x \\ 0 & f_y & o_y \\ 0 & 0 & 1 \end{bmatrix} \] We can then use this matrix to convert from pixel coordinates to camera coordinates using the following equation: \[ \begin{bmatrix} x_c \\ y_c \\ z_c \end{bmatrix} = \mathbf{K}^{-1} s \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} \] where \(s = z_c\) is the depth of the point along the optical axis. I implemented this function x_c = pixel_to_camera(K, uv, s) and once again made sure to include batched dimensions capability to speed up later computation.

Pixel to Ray

Now that we have the camera coordinates, we can construct the rays that represent how our camera sampled our scene. The ray is defined by an origin \(\mathbf{r}_o\) and a direction \(\mathbf{r}_d\). The origin is simply the location of the camera (\(\mathbf{r}_o = -\mathbf{R}^{-1}_{3\times3}t\)), and the direction is the normalized vector from the camera coordinates to the world coordinates. We can calculate this by simply choosing any point along the ray with depth equaling \(1\) and find its coordinate in world space \(\mathbf{X}_w\). We can then solve for the normalized ray direction using the following formula: \[ \mathbf{r}_d = \frac{\mathbf{X}_w - \mathbf{r}_o}{\|\mathbf{X}_w - \mathbf{r}_o\|_2} \] I implemented this function ray_o, ray_d = pixel_to_ray(K, c2w, uv) to return the ray directions for each pixel in the image, with once again support for batched dimensions.

2.2: Sampling

Now that we have all of our helper functions for converting from a camera coordinate into the corresponding rays, we can now sample along these rays to get our 3D space points. We can do this by choosing to get n_samples along our array (for my project, I mostly used n_samples=64) and uniformly sampling along the ray some distances away. For our lego scene, we can set near=2.0 and far=6.0, and then sample our 3D coordinates by the formula \(\mathbf{x} = \mathbf{r}_o + \mathbf{r_d}t\). However, this will always lead to the same set of 3D points, so to prevent overfitting, we add some small perturbation during the training stage by using the code t = t + (np.random.rand(t.shape)) * t_width where I set t_width = 0.02

2.3: Dataloading

Similar to the first part, we need to create our dataset loader to give us samples from our scene. In this case, we need to randomly sample pixels from our multiview images, and then convert said pixels into rays. We can than return the ray origin and ray direction (the inputs to our model) and the pixel value (the target of our model). In order to sample from multiview images, I flattened all pixels from all images and then did a global sampling to get \(N\) rays from all images. In this stage, I also ahd to account for the offset from image coordinate to pixel center, which I did by adding \(0.5\) to my uv pixel coordinate grid.

At this stage, we can verify the correctness of our functions for converting pixels into rays and our process of randomly sampling \(N\) rays from our multiview images dataset. I visualized the sampling process to ensure that my code was working as intended in terms of converting pixel coordinates into rays. I also visualized this process as sampling from one camera to further ensure that my helper functions were working as intended.

2.4: Nerual Radiance Field

Now that we have our datset samples we can use to train our model, we can create our model architecture. This model will now be attempting a much more complex task, and thus will require a more complex architecture. We will still be using a MLP, but this one will take in both the 3D coordinate and the viewing direction, and will predict an RGB value as well as a density. We will once again be using positional encoding, and will use a max frequency value of \(L=10\) for the coordinate point and a smaller value of \(L=4\) for the direction input vector. Here is the general architecture diagram:

Some other portions to note are that we are using a much deeper network this time, which means it will be beneficial for us to include a skip connection from the input to the midway part of the network predicting the position. This is a trick in deep neural networks that helps the model not forget about the input. We also once again use the Sigmoid activation function to constrain our output to the valid range of \([0, 1]\) for pixel colors.

2.5: Volume Rendering

The next important function we need to implement is the volume rendering function. This function will take in the outputs of our network (the density and rgb values) and will return the final pixel color for a given ray. We can do this by integrating the density and color values along the ray using the following formula: \[ C(\mathbf{r}) = \int_{t_{near}}^{t_{far}} T(t)\sigma(\mathbf{r}(t))\mathbf{c}(\mathbf{r}(t), \mathbf{d})dt, \quad \text{where} \ T(t) = exp\left(-\int_{t_{near}}^{t}\sigma(\mathbf{r}(s))ds \right) \] However, to implement this in practice, we can use the following sum approximation: \[ \hat{C}(\mathbf{r}) = \sum_{i=1}^{N} T(t)\sigma(\mathbf{r}(t))\mathbf{c}(\mathbf{r}(t), \mathbf{d})dt, \quad \text{where} \ T_i = \exp\left(-\sum^{i-1}_{j=1}\sigma_j\delta{j}\right) \] where \(\mathbf{c}_i\) is the color predicted by our network at sample location \(i\), \(T_i\) is the probabiliity of a ray not terminating before sample location i, and \(1 - e^{-\sigma_i\delta_i}\) is the probability of the ray terminating at sample location i.

Training the Model

Now that we have implemented all of the different parts of the model, we can finally train the model. I used a batch size of \(10000\) samples and trained for \(3000\) iterations using an Adam optimizer with learning rate \(0.0005\). This achieved a final training PSNR of \(26.062\) and a validation PSNR of \(24.96\). Here are some visualizations of our training process, and the PSNR curves throughout training:

As we can see, our model is able to learn the underlying structure of the scene and produce a reasonable reconstruction of the scene. We can now use this to produce completely novel views and generate the following spherical rendering of the lego scene: